딥러닝에서 사용하는 활성화함수
01 Jul 2018 | DeepLearning
딥러닝에서 사용하는 활성화 함수
딥러닝 네트워크에서는 노드에 들어오는 값들에 대해 곧바로 다음 레이어로 전달하지 않고 주로 비선형 함수를 통과시킨 후 전달한다. 이때 사용하는 함수를 활성화 함수(Activation Function) 이라 부른다.
여기서 주로 비선형 함수를 사용하는 이유는 선형함수를 사용할 시 층을 깊게 하는 의미가 줄어들기 때문이다.
선형함수인 h(x)=cx를 활성화함수로 사용한 3층 네트워크를 떠올려 보세요. 이를 식으로 나타내면 y(x)=h(h(h(x)))가 됩니다. 이는 실은 y(x)=ax와 똑같은 식입니다. a=c3이라고만 하면 끝이죠. 즉, 은닉층이 없는 네트워크로 표현할 수 있습니다. 뉴럴네트워크에서 층을 쌓는 혜택을 얻고 싶다면 활성화함수로는 반드시 비선형 함수를 사용해야 합니다.
- 밑바닥부터 시작하는 딥러닝 -
이번 포스트에서는 딥러닝에서 사용되는 활성화 함수들에 대해서 하나씩 알아보도록한다.
1. 시그모이드 함수 (Sigmoid)
시그모이드 함수는 Logistic 함수라 불리기도한다. 선형인 멀티퍼셉트론에서 비선형 값을 얻기 위해 사용하기 시작했다. 함수는 아래와 같이 구성된다.
시그모이드 함수와 시그모이드 함수의 미분함수를 그래프로 나타내면
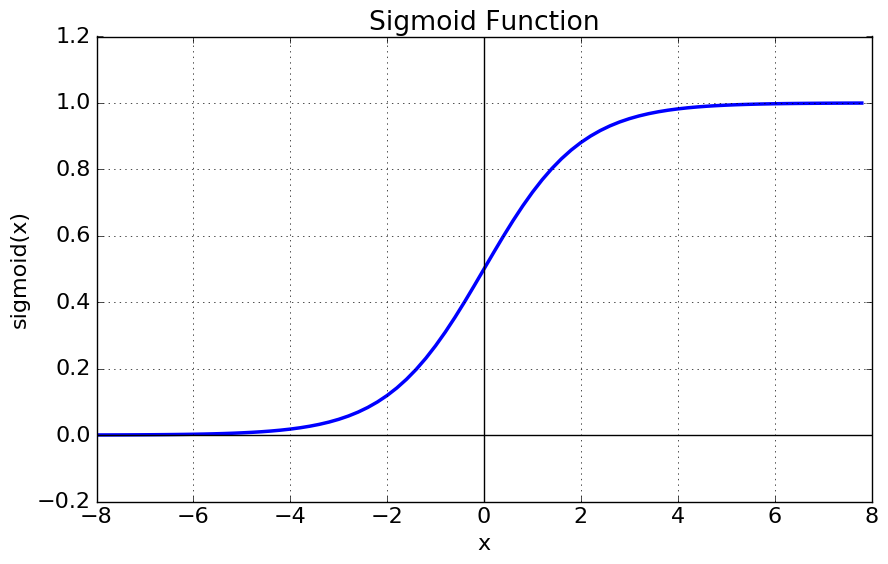
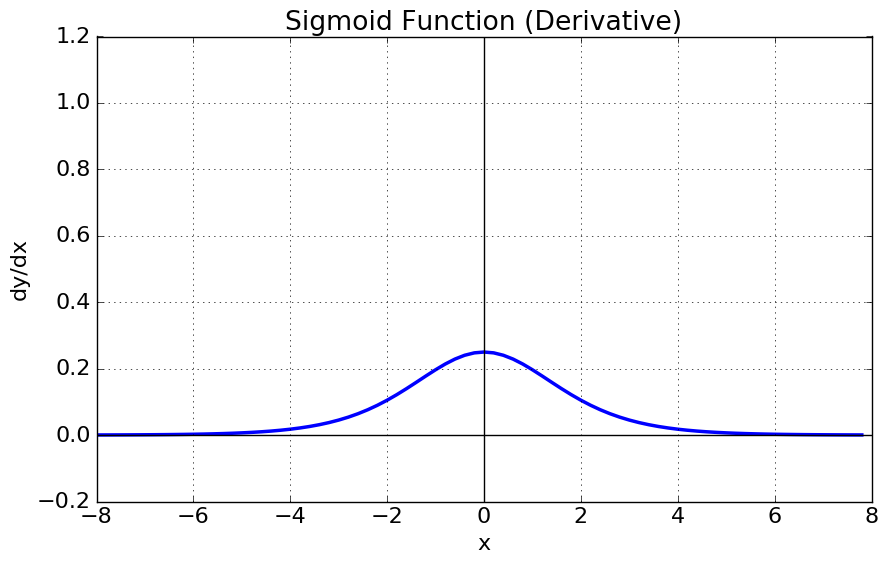
sigmoid에 대해 특징을 살펴보자.
- 우선 함수값이 (0, 1)로 제한된다.
- 중간 값은 $\frac{1}{2}$이다.
- 매우 큰 값을 가지면 함수값은 거의 1이며, 매우 작은 값을 가지면 거의 0이다.
이러한 특징을 가지는 sigmoid는 신경망 초기에는 많이 사용되었지만, 최근에는 아래의 단점들 때문에 사용하지 않는다.
- Gradient Vanishing 현상이 발생한다.
미분함수에 대해 $x=0$에서 최대값 $\frac{1}{4}$ 을 가지고, input값이 일정이상 올라가면 미분값이 거의 0에 수렴하게된다. 이는 $|x|$값이 커질 수록 Gradient Backpropagation시 미분값이 소실될 가능성이 크다.
- 함수값 중심이 0이 아니다.
함수값 중심이 0이 아니라 학습이 느려질 수 있다. 그 이유를 알아보면.
만약 모든 $x$값들이 같은 부호(ex. for all $x$ is positive) 라고 가정하고 아래의 파라미터 $w$에 대한 미분함수식을 살펴보자.
$\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{a}}\frac{\partial{a}}{\partial{w}}$
그리고 $\frac{\partial{a}}{\partial{w}}=x$이기 때문에,
$\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{a}}x$ 이다.
위 식에서 모든 $x$가 양수라면 결국 $\frac{\partial{L}}{\partial{w}}$는 $\frac{\partial{L}}{\partial{a}}$ 부호에 의해 결정된다. 따라서 한 노드에 대해 모든 파라미터$w$의 미분값은 모두 같은 부호를 같게된다. 따라서 같은 방향으로 update되는데 이러한 과정은 학습을 zigzag 형태로 만들어 느리게 만드는 원인이 된다.
- exp 함수 사용시 비용이 크다.
이러한 단점들 때문에 초기에는 자주 사용하는 활성화 함수였지만, 최근에는 자주 사용하지 않게 되었다.
2. $tanh$ 함수, (Hyperbolic tangent function)
하이퍼볼릭탄젠트란 쌍곡선 함수중 하나이다.
쌍곡선 함수 : 쌍곡선 함수란 삼각함수와 유사한 성질을 가지고, 표준 쌍곡선을 매개변수로 표시할 때 나오는 함수이다.
하이퍼볼릭탄젠트 함수는 시그모이드 함수를 transformation해서 얻을 수 있다.
-1 vertical shift & 1/2 horizontal squeeze & 2 vertical stretch
함수는 다음과 같이 정의된다.
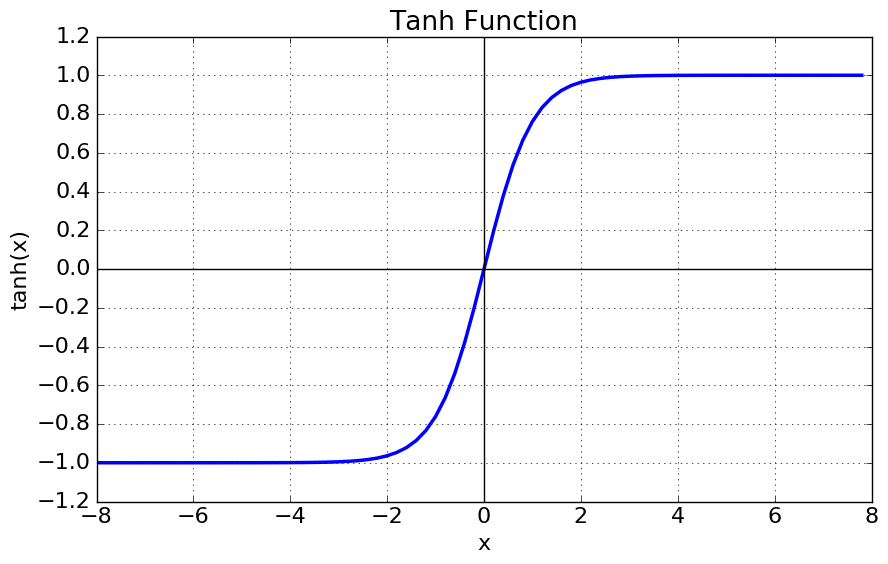
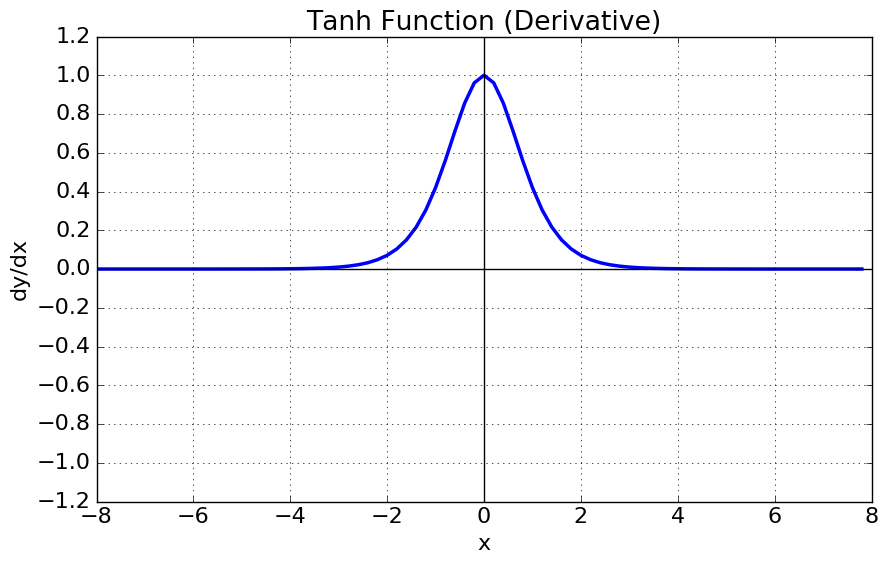
- tanh 함수는 함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결했다.
- 하지만 미분함수에 대해 일정값 이상 커질시 미분값이 소실되는 gradient vanishing 문제는 여전히 남아있다.
3. ReLU 함수 (Rectified Linear Unit)
ReLu함수는 최근 가장 많이 사용되는 활성화 함수이다. 함수는 아래와 같이 정의된다.
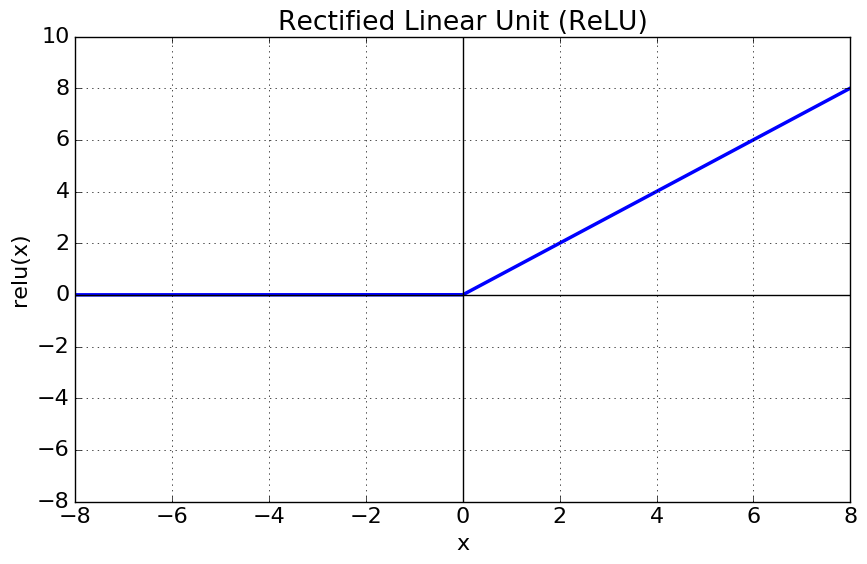
ReLU함수의 특징을 살펴보자.
- $x>0$ 이면 기울기가 1인 직선이고, $x<0$이면 함수값이 0이된다.
- sigmoid, tanh 함수와 비교시 학습이 훨씬 빨라진다.
- 연산 비용이 크지않고, 구현이 매우 간단하다.
- $x<0$인 값들에 대해서는 기울기가 0이기 때문에 뉴런이 죽을 수 있는 단점이 존재한다.
4. Leakly ReLU
leakly ReLU는 ReLU의 뉴런이 죽는(“Dying ReLu”)현상을 해결하기위해 나온 함수이다. 함수도 매우 간단한 형태로 다음과 같다.
위의 식에서 0.01대신 다른 매우 작은 값 사용 가능하다.
- Leakly ReLU는 음수의 $x$값에 대해 미분값이 0되지 않는다는 점을 제외하면 ReLU와 같은 특성을 가진다.
5. PReLU
Leakly ReLU와 거의 유사하지만 새로운 파라미터 $\alpha$ 를 추가하여 $x<0$에서 기울기를 학습할 수 있게 하였다.
6. Exponential Linear Unit(ELU)
ELU는 비교적 가장 최근에 나온 함수이다. Clevert et al. ,2015
ELU 의 특징은 다음과 같다.
- ReLU의 모든 장점을 포함한다.
- “Dying ReLU” 문제를 해결했다.
- 출력값이 거의 zero-centered에 가깝다
- 일반적인 ReLU와 달리 exp함수를 계산하는 비용이 발생한다.
7. Maxout 함수
Maxout 함수는 다음과 같다.
이 함수는 ReLU가 가지는 모든 장점을 가졌으며, dying ReLU문제 또한 해결한다. 하지만 계산량이 복잡하다는 단점이 있다.
결론
위와 같이 여러 활성화 함수가 있는데, 어떤 함수를 사용해야 할지에 대한 결론은 다음고 같다.
- 우선 가장 많이 사용되는 함수는 ReLU이다. 간단하고 사용이 쉽기 때문에 우선적으로 ReLU를 사용한다.
- ReLU를 사용한 이후 Leakly ReLU등 ReLU계열의 다른 함수도 사용 해본다.
- sigmoid의 경우에는 사용하지 않도록 한다.
- tanh의 경우도 큰 성능은 나오지 않는다.
참고
딥러닝에서 사용하는 활성화 함수
딥러닝 네트워크에서는 노드에 들어오는 값들에 대해 곧바로 다음 레이어로 전달하지 않고 주로 비선형 함수를 통과시킨 후 전달한다. 이때 사용하는 함수를 활성화 함수(Activation Function) 이라 부른다.
여기서 주로 비선형 함수를 사용하는 이유는 선형함수를 사용할 시 층을 깊게 하는 의미가 줄어들기 때문이다.
선형함수인 h(x)=cx를 활성화함수로 사용한 3층 네트워크를 떠올려 보세요. 이를 식으로 나타내면 y(x)=h(h(h(x)))가 됩니다. 이는 실은 y(x)=ax와 똑같은 식입니다. a=c3이라고만 하면 끝이죠. 즉, 은닉층이 없는 네트워크로 표현할 수 있습니다. 뉴럴네트워크에서 층을 쌓는 혜택을 얻고 싶다면 활성화함수로는 반드시 비선형 함수를 사용해야 합니다. - 밑바닥부터 시작하는 딥러닝 -
이번 포스트에서는 딥러닝에서 사용되는 활성화 함수들에 대해서 하나씩 알아보도록한다.
1. 시그모이드 함수 (Sigmoid)
시그모이드 함수는 Logistic 함수라 불리기도한다. 선형인 멀티퍼셉트론에서 비선형 값을 얻기 위해 사용하기 시작했다. 함수는 아래와 같이 구성된다.
시그모이드 함수와 시그모이드 함수의 미분함수를 그래프로 나타내면


sigmoid에 대해 특징을 살펴보자.
- 우선 함수값이 (0, 1)로 제한된다.
- 중간 값은 $\frac{1}{2}$이다.
- 매우 큰 값을 가지면 함수값은 거의 1이며, 매우 작은 값을 가지면 거의 0이다.
이러한 특징을 가지는 sigmoid는 신경망 초기에는 많이 사용되었지만, 최근에는 아래의 단점들 때문에 사용하지 않는다.
- Gradient Vanishing 현상이 발생한다. 미분함수에 대해 $x=0$에서 최대값 $\frac{1}{4}$ 을 가지고, input값이 일정이상 올라가면 미분값이 거의 0에 수렴하게된다. 이는 $|x|$값이 커질 수록 Gradient Backpropagation시 미분값이 소실될 가능성이 크다.
- 함수값 중심이 0이 아니다. 함수값 중심이 0이 아니라 학습이 느려질 수 있다. 그 이유를 알아보면. 만약 모든 $x$값들이 같은 부호(ex. for all $x$ is positive) 라고 가정하고 아래의 파라미터 $w$에 대한 미분함수식을 살펴보자. $\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{a}}\frac{\partial{a}}{\partial{w}}$ 그리고 $\frac{\partial{a}}{\partial{w}}=x$이기 때문에, $\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{a}}x$ 이다. 위 식에서 모든 $x$가 양수라면 결국 $\frac{\partial{L}}{\partial{w}}$는 $\frac{\partial{L}}{\partial{a}}$ 부호에 의해 결정된다. 따라서 한 노드에 대해 모든 파라미터$w$의 미분값은 모두 같은 부호를 같게된다. 따라서 같은 방향으로 update되는데 이러한 과정은 학습을 zigzag 형태로 만들어 느리게 만드는 원인이 된다.
- exp 함수 사용시 비용이 크다.
이러한 단점들 때문에 초기에는 자주 사용하는 활성화 함수였지만, 최근에는 자주 사용하지 않게 되었다.
2. $tanh$ 함수, (Hyperbolic tangent function)
하이퍼볼릭탄젠트란 쌍곡선 함수중 하나이다.
쌍곡선 함수 : 쌍곡선 함수란 삼각함수와 유사한 성질을 가지고, 표준 쌍곡선을 매개변수로 표시할 때 나오는 함수이다.
하이퍼볼릭탄젠트 함수는 시그모이드 함수를 transformation해서 얻을 수 있다.
-1 vertical shift & 1/2 horizontal squeeze & 2 vertical stretch
함수는 다음과 같이 정의된다.


- tanh 함수는 함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결했다.
- 하지만 미분함수에 대해 일정값 이상 커질시 미분값이 소실되는 gradient vanishing 문제는 여전히 남아있다.
3. ReLU 함수 (Rectified Linear Unit)
ReLu함수는 최근 가장 많이 사용되는 활성화 함수이다. 함수는 아래와 같이 정의된다.

ReLU함수의 특징을 살펴보자.
- $x>0$ 이면 기울기가 1인 직선이고, $x<0$이면 함수값이 0이된다.
- sigmoid, tanh 함수와 비교시 학습이 훨씬 빨라진다.
- 연산 비용이 크지않고, 구현이 매우 간단하다.
- $x<0$인 값들에 대해서는 기울기가 0이기 때문에 뉴런이 죽을 수 있는 단점이 존재한다.
4. Leakly ReLU
leakly ReLU는 ReLU의 뉴런이 죽는(“Dying ReLu”)현상을 해결하기위해 나온 함수이다. 함수도 매우 간단한 형태로 다음과 같다.
위의 식에서 0.01대신 다른 매우 작은 값 사용 가능하다.
- Leakly ReLU는 음수의 $x$값에 대해 미분값이 0되지 않는다는 점을 제외하면 ReLU와 같은 특성을 가진다.
5. PReLU
Leakly ReLU와 거의 유사하지만 새로운 파라미터 $\alpha$ 를 추가하여 $x<0$에서 기울기를 학습할 수 있게 하였다.
6. Exponential Linear Unit(ELU)
ELU는 비교적 가장 최근에 나온 함수이다. Clevert et al. ,2015
ELU 의 특징은 다음과 같다.
- ReLU의 모든 장점을 포함한다.
- “Dying ReLU” 문제를 해결했다.
- 출력값이 거의 zero-centered에 가깝다
- 일반적인 ReLU와 달리 exp함수를 계산하는 비용이 발생한다.
7. Maxout 함수
Maxout 함수는 다음과 같다.
이 함수는 ReLU가 가지는 모든 장점을 가졌으며, dying ReLU문제 또한 해결한다. 하지만 계산량이 복잡하다는 단점이 있다.
결론
위와 같이 여러 활성화 함수가 있는데, 어떤 함수를 사용해야 할지에 대한 결론은 다음고 같다.
- 우선 가장 많이 사용되는 함수는 ReLU이다. 간단하고 사용이 쉽기 때문에 우선적으로 ReLU를 사용한다.
- ReLU를 사용한 이후 Leakly ReLU등 ReLU계열의 다른 함수도 사용 해본다.
- sigmoid의 경우에는 사용하지 않도록 한다.
- tanh의 경우도 큰 성능은 나오지 않는다.
참고
Comments