파라미터 최적화
02 Jul 2018 | DeepLearning
파라미터 최적화 (Parameter Optimization)
딥러닝 학습의 기본은 파라미터들을 최적의 값으로 빠르고 정확하게 수렴하는 것을 목적으로 한다.
파라미터를 최적화 하는 방법에는 여러 방법들이 있다. Gradient Descent를 기반으로한 방법들, 모멘텀 방식을 도입한 학습 방법 그 외에도 AdaGrad, RMSProp, Adam까지 여러 방법들이 존재한다.
최적화 방법 선택에 따라 최적화까지의 시간에 차이는 매우 크게 난다. 따라서 최적화 방법을 잘 선택하는 것이 매우 중요한데, 그럼 방법들에 대해서 하나씩 알아보도록 한다.
1. Gradient Descent기반 방식들
파라미터 최적화 방법으로 가장 널리 알려진 방법은 그라디언트 디센트(Gradient Descent)방식이다. 이 방법은 현재의 미분값을 기반으로해서 파라미터가 업데이트 해야할 방향과 크기를 설정합니다. 업데이트 수식을 아래와 같습니다.
여기서 $\theta$는 학습할 파라미터를 뜻하고, $\eta$는 미분값을 기준으로 update할 시 어느정도의 크기로 학습할 것인가를 나타내는 학습률(Learning rate)을 뜻한다. $L$은 모델의 손실함수(Cost Function)을 뜻한다.
따라서 위식에 따르면, 파라미터를 파라미터로 손실함수를 미분한 값 반대방향으로 $\eta\frac{\partial L}{\partial \theta}$크기만큼 이동하라는 것을 뜻한다.
여기까지가 Gradient Descent의 기본에 대해 설명한 것이고, 이 방법을 기반으로 한 방법들에 대해서 하나씩 살펴보도록 하자.
1-1)Batch Gradient Descent
Batch Gradient Descent 방식이란, 모든 데이터셋을 하나의 batch로 보고 전체의 미분값을 평균하여 1에폭동안 update를 딱 한번 수행하는 방식이다. 속도가 느리다는 단점이 있지만, 최적값을 찾을 수 있다는 장점이 있다.
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
1-2)Stochastic Gradient Descent(SGD)
확률적 경사하강법인 Stocchastic Gradient Descent(SGD)는 각 iteration에서 하나의 example만을 뽑아서 학습시키는 방법이다. 엄밀하게 SGD는 하나의 data만을 뽑아서 학습시키는 방법이지만, 랜덤하게 n개의 데이터를 뽑아 update시키는 방법인 MGD(Mini-Batch Gradient Descent)방식 대신 SGD로 표현해서 사용하기도 합니다. SGD사용은 속도를 훨씬 빠르게 한다는 장점이있고, 아래와 같은 특징들이 있다.
- for-loop을 돌기전 데이터 셋을 랜덤하게 Suffle할 필요가 있다.
- SGD방식은 BGD방식에 비해 최적화로 가는 과정에서 Noise가 많이 발생할 수 있다.
for i in range(nb_epochs):
np.random.shuffle(data)
for iter in range(start_iter, num_iter):
params_grad = evaluate_gradient(loss_function, data[0], params)
params = params - learning_rate * params_grad
1-3)Mini-Batch Gradient Descent
미니배치 방식의 Gradient Descent 방식은 일정크기 n만큼의 데이터에 대해서 미분값을 평균하여 update하는 방식이다. SGD에 비해 안정적이며, 속도도 BGD에 비해 빨라 대부분 많이 사용하는 방식이다.
for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate * params_grad
2. Momentum
2-1) Momentum
모멘텀이란 물리학 용어로 물체의 속도와 질량에 관련된 운동량을 뜻한다. 아래 그림을 보자
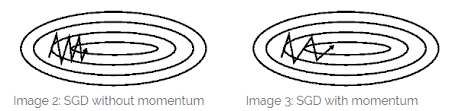왼쪽 그림의 경우 위 아래 방향으로는 계속해서 반복되는 운동을 하는 것을 볼 수 있는데, 오른쪽으로는 한방향으로만 움직인다. 이러한 경우 오른쪽 방향으로의 운동량이 계속해서 누적된다는 것을 확인 할 수 있다. 따라서 Momentum 방식을 따르면 오른쪽 그림과 같이 위 아래 반복적인 움직임은 여전히 보여주지만 오른쪽으로 지속적인 움직임이 누적되서 더욱 빠르게 최적화가 되는 것을 확인할 수 있다.
모멘텀의 수식은 다음과 같다.
GD방식과는 달리 새로운 하이퍼 파라미터 $\mu$와 변수인 $v$가 새롭게 추가되었다.
위 수식을 보면 위의 모멘텀을 적용한 학습 경과가 이해될 것이다. 오른쪽 방향으로의 미분값은 계속해서 $v$에 더해져서 더욱 큰 값을 갖게 되어 빠르게 이동할 수 있는 것이다.
param_grad = evaluate_gradient(loss_function, data, params)
v = mu * v - learning_rate * param_grad
param = v + param
2-2) Nesterov 모멘텀 (Nesterov Momentum)
Nesterov Momentum 방식은 최근 많은 주목을 받은 방식으로, Momentum과는 약간 다르다. Convex function에서는 이 함수가 이론적으로 최적화에 유리하며, 일반적으로도 Momentum 방식보다는 좋다는 의견이 있다.
Nestrov 모멘텀의 방식은 모멘텀방식에서 현재위치인 $\theta$에서 미분값을 구하는 것이 아니라, 우리가 이동할 위치인 $\theta+\mu v$의 위치에서의 미분값을 계산하는 것이 모멘텀 방식과의 다른점이다.
그림을 통해 살펴보자.
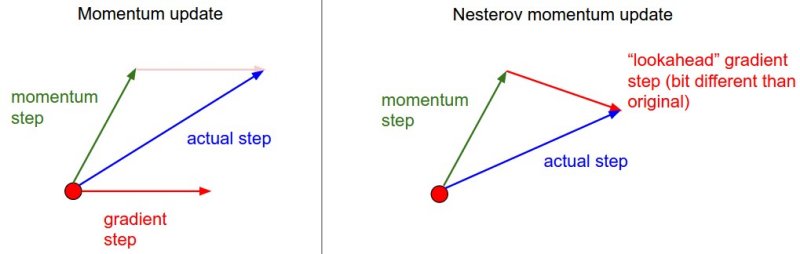momentum방식에서는 빨간점에서의 미분값을 계산해 update를 시켰으나, Nestrov 방식에서는 초록색 벡터의 끝점에서 미분값을 계산해 update를 시킨다는 것을 의미한다.
아래 식을 보면 조금 더 명확하게 이해될 것이다.
params_ahead = params + mu * v
params_grad_ahead = evaluate_gradient(loss_function, data, params_ahead)
v = mu * v - learning_rate * params_grad_ahead
params = v + params
3. Per-parameter adaptive learning rate 방법들
이때까지의 파라미터 최적화 방법들에서는 모든 파라미터에 대해 똑같은 학습 속도를 적용 하였다. 그러나 Per-parameter adaptive learning rate 방법들에서는 각 파라미터에 대해 adaptive한 학습 속도를 적용한다.
3-1) AdaGrad
AdaGra는 Adaptive gradient based 방식으로 Duchi et al.에서 처음으로 소개했다.
AdaGrad에서는 이전 update에서 update가 많이 된 파라미터들에 대해서는 학습량을 줄이는 방법을 사용한다. 수식은 아래와 같다.
params_grad = evaluate_gradient(loss_function, data, params)
h = h + params_grad**2
params = params - learning_rate / (np.sqrt(h) + eps) * params_grad
코드를 확인해보면, 수식과는 약간 다른점을 확인 할 수 있다. 아래 식의 $\sqrt{h}$ 값에 eps라는 변수가 더해져 있다. 이 값은 $h$가 0이 되거나 0에 너무 가깝게 되서 전체값이 너무 커져버리는 상황을 방지하기위한 변수로 주로 1e-4에서 1e-8정도의 값을 준다.
하지만 이 방법은 지나치게 learning rate을 낮추는 경향이 있어 deep learning model에 적용 시 잘 학습이 되지 않는 경향이 있어 자주 사용하지 않는다.
3-2) RMSProp
AdaGrad에서는 $L$을 parameter로 미분한 값을 제곱한 값을 계속 더한 것을 update시 미분값에 나눠준다. 이러한 과정을 계속해서 반복하면, 최종적으로 upadate 값이 0에 수렴해 학습이 불가능해진다.
RMSProp은 이러한 문제를 개선한 방법으로 지수 이동 평균(Exponential moving average)을 사용하였다.
지수 이동 평균이란 과거의 모든 기간을 계산 대상으로 하며, 최근의 데이터에 더 높은 가중치를 부여한는 일종의 가중 이동 평균 방법이다.
params_grad = evaluate_gradient(loss_function, data, params)
h = decay_rate * h + (1 - decay_rate) * params_grad**2
params = params - learning_rate / (np.sqrt(h) + eps) * params_grad
위 코드에서 decay_rate는 hyper-parameter로 사용자가 직접 정해야 하며, 주로 0.9, 0.99, 0.999중 하나를 선택해 사용한다.
3-3) Adam
모멘텀 기법은 운동량에 착안해서 만든 방법이고, RMSProp은 파라미터 개별마다 Adaptive한 학습방식이다. Adam 은 이 두방법을 합친 방법이라 할 수 있다.
실전에서 Adam은 가장 기본적으로 사용되는 방법이고, 성능이 좋아 많이 사용하는 방법이다.
수식은 다음과 같다.
사용자가 직접 설정해야 할 Hyper parameter는 $\beta_{1}$과 $\beta_{2}$, 그리고 $\epsilon$으로 3가지다.
보통 $\beta_{1}=0.9$, $\beta_{2}=0.999$, $\epsilon$ 값으로는 $1e-8$ 로 설정한다.
파라미터 최적화 방법 비교
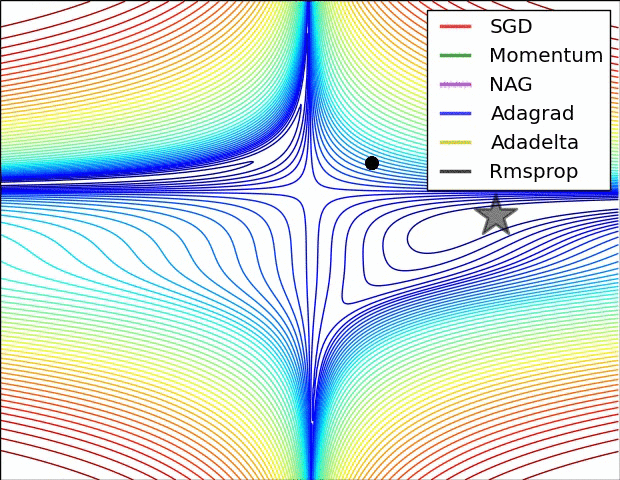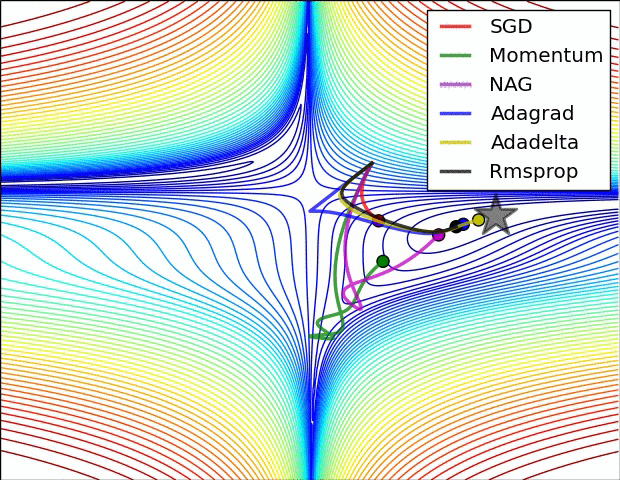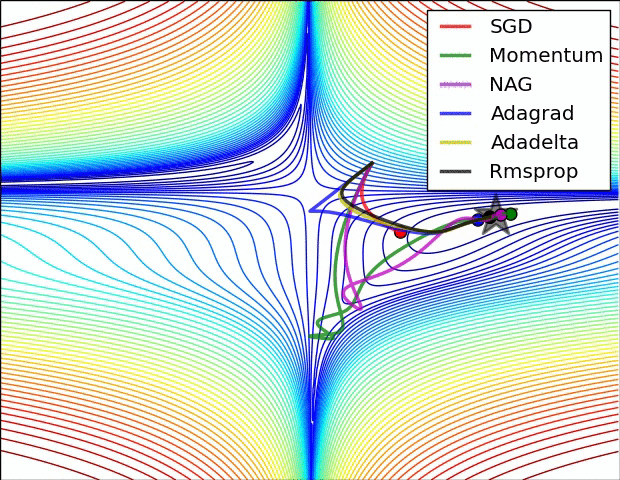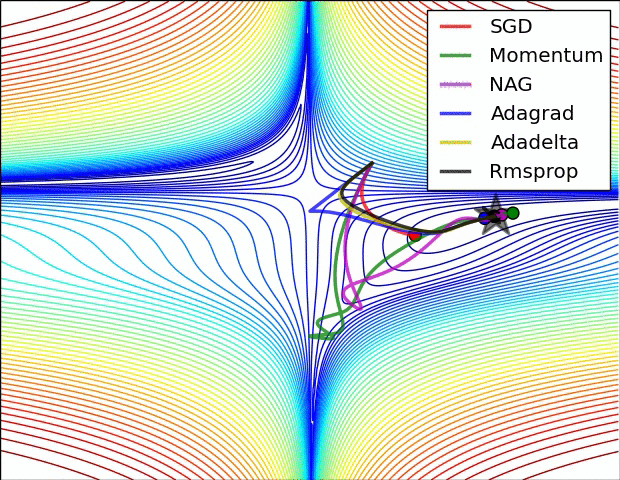
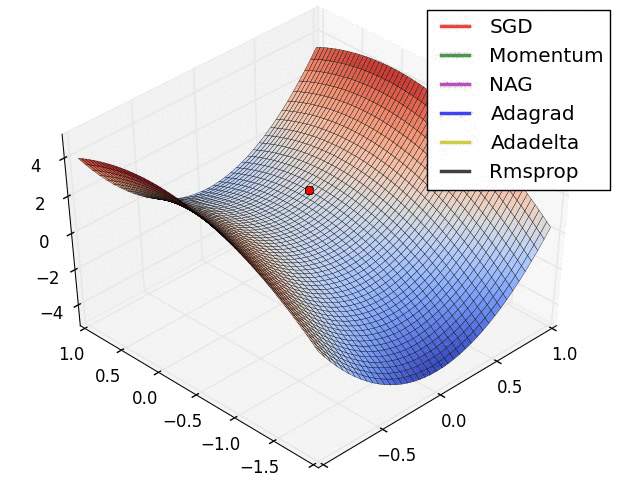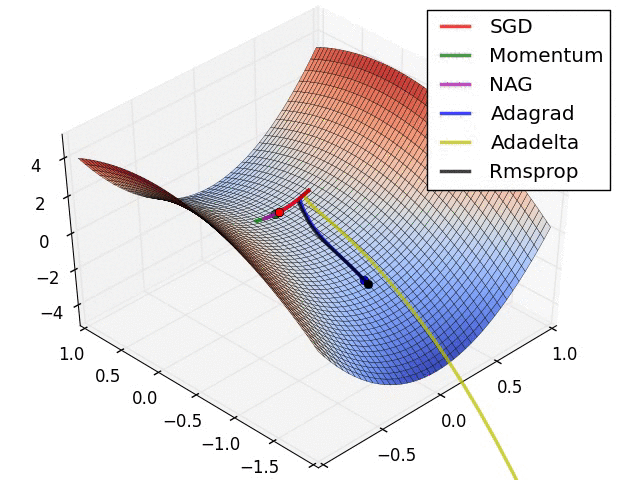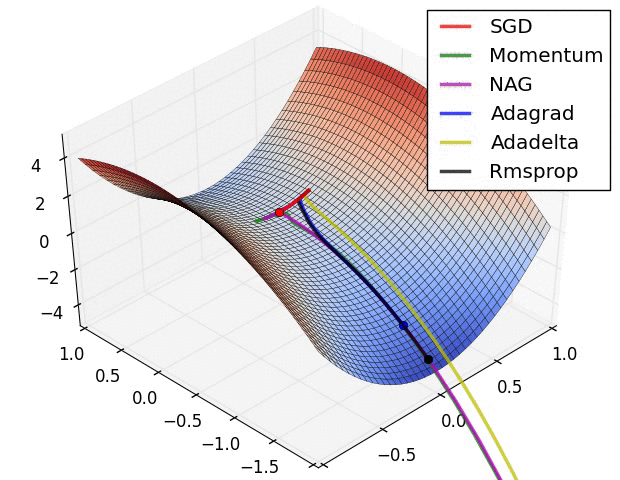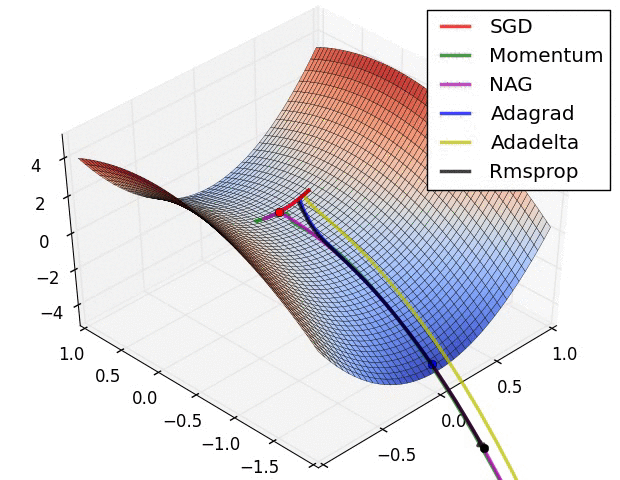
출처
파라미터 최적화 (Parameter Optimization)
딥러닝 학습의 기본은 파라미터들을 최적의 값으로 빠르고 정확하게 수렴하는 것을 목적으로 한다. 파라미터를 최적화 하는 방법에는 여러 방법들이 있다. Gradient Descent를 기반으로한 방법들, 모멘텀 방식을 도입한 학습 방법 그 외에도 AdaGrad, RMSProp, Adam까지 여러 방법들이 존재한다. 최적화 방법 선택에 따라 최적화까지의 시간에 차이는 매우 크게 난다. 따라서 최적화 방법을 잘 선택하는 것이 매우 중요한데, 그럼 방법들에 대해서 하나씩 알아보도록 한다.
1. Gradient Descent기반 방식들
파라미터 최적화 방법으로 가장 널리 알려진 방법은 그라디언트 디센트(Gradient Descent)방식이다. 이 방법은 현재의 미분값을 기반으로해서 파라미터가 업데이트 해야할 방향과 크기를 설정합니다. 업데이트 수식을 아래와 같습니다.
여기서 $\theta$는 학습할 파라미터를 뜻하고, $\eta$는 미분값을 기준으로 update할 시 어느정도의 크기로 학습할 것인가를 나타내는 학습률(Learning rate)을 뜻한다. $L$은 모델의 손실함수(Cost Function)을 뜻한다. 따라서 위식에 따르면, 파라미터를 파라미터로 손실함수를 미분한 값 반대방향으로 $\eta\frac{\partial L}{\partial \theta}$크기만큼 이동하라는 것을 뜻한다.
여기까지가 Gradient Descent의 기본에 대해 설명한 것이고, 이 방법을 기반으로 한 방법들에 대해서 하나씩 살펴보도록 하자.
1-1)Batch Gradient Descent
Batch Gradient Descent 방식이란, 모든 데이터셋을 하나의 batch로 보고 전체의 미분값을 평균하여 1에폭동안 update를 딱 한번 수행하는 방식이다. 속도가 느리다는 단점이 있지만, 최적값을 찾을 수 있다는 장점이 있다.
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
1-2)Stochastic Gradient Descent(SGD)
확률적 경사하강법인 Stocchastic Gradient Descent(SGD)는 각 iteration에서 하나의 example만을 뽑아서 학습시키는 방법이다. 엄밀하게 SGD는 하나의 data만을 뽑아서 학습시키는 방법이지만, 랜덤하게 n개의 데이터를 뽑아 update시키는 방법인 MGD(Mini-Batch Gradient Descent)방식 대신 SGD로 표현해서 사용하기도 합니다. SGD사용은 속도를 훨씬 빠르게 한다는 장점이있고, 아래와 같은 특징들이 있다.
- for-loop을 돌기전 데이터 셋을 랜덤하게 Suffle할 필요가 있다.
- SGD방식은 BGD방식에 비해 최적화로 가는 과정에서 Noise가 많이 발생할 수 있다.
for i in range(nb_epochs): np.random.shuffle(data) for iter in range(start_iter, num_iter): params_grad = evaluate_gradient(loss_function, data[0], params) params = params - learning_rate * params_grad
1-3)Mini-Batch Gradient Descent
미니배치 방식의 Gradient Descent 방식은 일정크기 n만큼의 데이터에 대해서 미분값을 평균하여 update하는 방식이다. SGD에 비해 안정적이며, 속도도 BGD에 비해 빨라 대부분 많이 사용하는 방식이다.
for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate * params_grad
2. Momentum
2-1) Momentum
모멘텀이란 물리학 용어로 물체의 속도와 질량에 관련된 운동량을 뜻한다. 아래 그림을 보자
왼쪽 그림의 경우 위 아래 방향으로는 계속해서 반복되는 운동을 하는 것을 볼 수 있는데, 오른쪽으로는 한방향으로만 움직인다. 이러한 경우 오른쪽 방향으로의 운동량이 계속해서 누적된다는 것을 확인 할 수 있다. 따라서 Momentum 방식을 따르면 오른쪽 그림과 같이 위 아래 반복적인 움직임은 여전히 보여주지만 오른쪽으로 지속적인 움직임이 누적되서 더욱 빠르게 최적화가 되는 것을 확인할 수 있다.
모멘텀의 수식은 다음과 같다.
GD방식과는 달리 새로운 하이퍼 파라미터 $\mu$와 변수인 $v$가 새롭게 추가되었다. 위 수식을 보면 위의 모멘텀을 적용한 학습 경과가 이해될 것이다. 오른쪽 방향으로의 미분값은 계속해서 $v$에 더해져서 더욱 큰 값을 갖게 되어 빠르게 이동할 수 있는 것이다.
param_grad = evaluate_gradient(loss_function, data, params)
v = mu * v - learning_rate * param_grad
param = v + param
2-2) Nesterov 모멘텀 (Nesterov Momentum)
Nesterov Momentum 방식은 최근 많은 주목을 받은 방식으로, Momentum과는 약간 다르다. Convex function에서는 이 함수가 이론적으로 최적화에 유리하며, 일반적으로도 Momentum 방식보다는 좋다는 의견이 있다.
Nestrov 모멘텀의 방식은 모멘텀방식에서 현재위치인 $\theta$에서 미분값을 구하는 것이 아니라, 우리가 이동할 위치인 $\theta+\mu v$의 위치에서의 미분값을 계산하는 것이 모멘텀 방식과의 다른점이다.
그림을 통해 살펴보자.
momentum방식에서는 빨간점에서의 미분값을 계산해 update를 시켰으나, Nestrov 방식에서는 초록색 벡터의 끝점에서 미분값을 계산해 update를 시킨다는 것을 의미한다.
아래 식을 보면 조금 더 명확하게 이해될 것이다.
params_ahead = params + mu * v
params_grad_ahead = evaluate_gradient(loss_function, data, params_ahead)
v = mu * v - learning_rate * params_grad_ahead
params = v + params
3. Per-parameter adaptive learning rate 방법들
이때까지의 파라미터 최적화 방법들에서는 모든 파라미터에 대해 똑같은 학습 속도를 적용 하였다. 그러나 Per-parameter adaptive learning rate 방법들에서는 각 파라미터에 대해 adaptive한 학습 속도를 적용한다.
3-1) AdaGrad
AdaGra는 Adaptive gradient based 방식으로 Duchi et al.에서 처음으로 소개했다. AdaGrad에서는 이전 update에서 update가 많이 된 파라미터들에 대해서는 학습량을 줄이는 방법을 사용한다. 수식은 아래와 같다.
params_grad = evaluate_gradient(loss_function, data, params)
h = h + params_grad**2
params = params - learning_rate / (np.sqrt(h) + eps) * params_grad
코드를 확인해보면, 수식과는 약간 다른점을 확인 할 수 있다. 아래 식의 $\sqrt{h}$ 값에 eps라는 변수가 더해져 있다. 이 값은 $h$가 0이 되거나 0에 너무 가깝게 되서 전체값이 너무 커져버리는 상황을 방지하기위한 변수로 주로 1e-4에서 1e-8정도의 값을 준다.
하지만 이 방법은 지나치게 learning rate을 낮추는 경향이 있어 deep learning model에 적용 시 잘 학습이 되지 않는 경향이 있어 자주 사용하지 않는다.
3-2) RMSProp
AdaGrad에서는 $L$을 parameter로 미분한 값을 제곱한 값을 계속 더한 것을 update시 미분값에 나눠준다. 이러한 과정을 계속해서 반복하면, 최종적으로 upadate 값이 0에 수렴해 학습이 불가능해진다. RMSProp은 이러한 문제를 개선한 방법으로 지수 이동 평균(Exponential moving average)을 사용하였다.
지수 이동 평균이란 과거의 모든 기간을 계산 대상으로 하며, 최근의 데이터에 더 높은 가중치를 부여한는 일종의 가중 이동 평균 방법이다.
params_grad = evaluate_gradient(loss_function, data, params)
h = decay_rate * h + (1 - decay_rate) * params_grad**2
params = params - learning_rate / (np.sqrt(h) + eps) * params_grad
위 코드에서 decay_rate는 hyper-parameter로 사용자가 직접 정해야 하며, 주로 0.9, 0.99, 0.999중 하나를 선택해 사용한다.
3-3) Adam
모멘텀 기법은 운동량에 착안해서 만든 방법이고, RMSProp은 파라미터 개별마다 Adaptive한 학습방식이다. Adam 은 이 두방법을 합친 방법이라 할 수 있다. 실전에서 Adam은 가장 기본적으로 사용되는 방법이고, 성능이 좋아 많이 사용하는 방법이다.
수식은 다음과 같다.
사용자가 직접 설정해야 할 Hyper parameter는 $\beta_{1}$과 $\beta_{2}$, 그리고 $\epsilon$으로 3가지다. 보통 $\beta_{1}=0.9$, $\beta_{2}=0.999$, $\epsilon$ 값으로는 $1e-8$ 로 설정한다.
파라미터 최적화 방법 비교
출처
Comments