Chapter 4: Recurrent Neural Networks and Gated Recurrent Units
18 Jul 2018 | NLP
Chapter 4
Recurrent Neural Networks and Gated Recurrent Units
이 내용은 Newyork University의 조경현교수님의 NLP_DL강의 lecture note중 Recurrent Neural Networks and Gated Recurrent Units단원을 정리한 내용이다.
이번 단원에는 몇 개의 단원에서 생략된 부분이 있습니다. 전체적인 흐름에 있어선는 문제가 없다고 판단되는 선에서 생략했으나, 혹시나 생략된 부분에 알고 싶으신 분들은 lecture note를 참고해 주시기 바랍니다.
4.1 Recurrent Neural Network
기존의 우리가 배운 Neural Network에서는 input $x$가 고정 size의 scalar 혹은 vector였다. 그러나 여기서는 input $x$가 고정 size라는 가정을 없에고 가변 길이의 input, 즉 sequence를 다루는 법을 알아 볼 것이다.
우선 가장 간단한 형태인 binary값을 가지는 sequence에 대해서 살펴보자. 1 혹은 0 만을 가지는 sequence에 대해서 1의 개수를 알고 싶다면 어떻게 해야 할까?
이 때 사용해야 하는 함수는 다음과 같다.

위 알고리즘을 사용한다면 sequence에서의 1값이 몇번인지 확인 할 수 있을 것 이다.
ADD1 알고리즘의 중요한 특징은 다음과 같다.
- ‘1’의 개수를 새는 memory $s$
- sequence의 각 symbol에 ‘하나씩’ 적용된다.(차례대로)
이 두가지 특성 때문에 가변길이의 sequence에 사용될 수 있다. 이 ADD1 알고리즘의 idea(‘memory’&’recursive function’)를 일반화 하자.
가장 일반적인 예는 컴퓨터이다. 특히 컴퓨터에서 CPU가 명령어를 처리하는 과정에 위의 idea가 사용되었다. (CPU : sequence of instruction($x_i$))
그러나 우리가 필요한 것은 학습을 위한 Network이므로 parametric recursive function (NLP를 하기 위한 언어적 symbol을 읽을 수 있는)가 필요하다.
Parametric recursive function을 만들기 위해 필요한 것에 대해 먼저 생각해보자. 우선 memory역할을 할 vector가 필요하다 이를 $h\in\mathbb{R}^{d_h}$라 하자. 그리고 recursive한 fucntion은 input symbol과 memory $h$ 둘 다 input으로 받는다. 이후 function을 통과시켜 memory를 업데이트 시킨 후 return한다. 각각의 memory $h$를 구분하기 위해 time index을 사용한다. ($h_t,h_{t-1},…$) 이러한 recursive한 fucntion은 다음과 같이 작성될 것이다.
그리고 함수 $f()$는 다음과 같이 정의한다.
- $\phi(~~)$함수는 input symbol을 d dimension으로 바꿔주는 함수.
- $W\in\mathbb{R}^{d_h\times d}$
- $U\in\mathbb{R}^{d_h\times d_h}$
- $g$는 element-wise nonlinear한 activation function뭐든 사용가능 하다.(e.g $tanh, sigmoid$)
위의 함수를 통과하게 되면 $d_h$ dimension을 가지는 vector가 된다. 이 값은 다음 값의 memory로 사용되거나 output으로 사용된다.
함수에 대해서 정의했으므로 이제는 두 가지 분류로 문제를 구분할 것이다.
- fixed-size의 output $y$
- variable length sequence의 output $y$
4.1.1 Fixed size output
기본적인 binary classification의 경우에 대해서 살펴보자. 가장 대표적인 binary classification의 예는 글에 대해 positive(1), negative(0) 감정을 평가하는 문제다. 이러한 문제는 결과가 0 혹은 1이므로 bernoulli distribution이라 생각할 수 있다. 따라서 우리는 distribution의 유일한 parameter인 $\mu$만 구하면 된다. 따라서 $\mu$를 다음과 같이 정의한다.
- 마지막 memory인 $h_l$사용
- 활성화 함수로 sigmoid 함수 사용한다.(0~1값을 출력해야 하므로)
따라서 전체적인 계산은 다음과 같이 한다.
여기서 가장 최초의 memory인 $h_0$는 보통 all zero vector를 사용한다. 그리고 $\mathbf{W, U}$는 shared parameter다.
또 다른 예를 들어 보자. 이번에도 감정 분석 문제이지만, 이번에는 분석해야 할 class가 3개, 즉 positive(1), neutral(2), neagtive(3)으로 분석해야 하는 문제에 대해 살펴보자. 이번에는 출력값이 $\mu$값 1개가 아닌, 3개의 $\mu$를 가지는 $\mathbf{\mu}= [\mu_1, \mu_2, \mu_3]$벡터를 출력으로 구해야 한다.
구하는 방식은 이전과 거의 비슷하지만 마지막 output을 뽑아낼 때 sigmoid가 아닌 softmax를 사용해야 한다.
4.1.4 Variable length output
가변길이의 output은 sequence형태가 된다.
이러한 문제의 대표적인 예는 POS tagging 문제다. 각 input $x$에 대해 noun, verb, adjective, others에 대한 각각의 확률값을 출력하는 문제다.
이러한 경우에는 각각의 step에서 memory를 각 step의 출력층, 다음 step 두 곳 모두로 보낸다. 각각의 layer에서의 출력은 다음과 같이 계산한다.
학습을 위해 각 step의 Cost는 다음과 같이 정의한다.
Cost함수에 대해서 간단히 설명을 하자면 I함수 때문에 정답 label을 가지는 단어에 대해서만 log값을 계산한다. 이 때 -log함수이기 떄문에 1에 가까울수록 적은 Cost를 가지고, 0에 가까울 수록 매우 큰 Cost를 가지게 된다. 따라서 전체적으로 우리는 Cost를 minimize하는 방향으로 가야 한다.
Cost 계산을 실제로 할때는 총합을 계산해서 학습을 시킨다.
위의 전체 cost를 minimize하는 방향으로 Network를 학습시켜야 한다.
결국 이 식이 목표하는 것은
이 조건부 확률을 최대화 하는 것이다. 그러나 위의 식을 단순히 cost함수로 표현을 하기에는 각각의 $x$ value들이 independent하다는 가정이 필요하다. 그러나 대부분의 경우에 그러한 가정을 사용하기에는 무리가 있다. 예를 들어 POS tagging 의 경우에만 봐도 명사 뒤에는 동사가 나올 확률이 높아진다. 이런 경우만 봐도 $x$ value들은 independent라고 하기는 어렵다.
따라서 우리는 condition으로 $y$의 값도 사용함으로써 독립 가정에 의한 격차를 줄인다.
즉, 아래와 같은 식으로 계산한다.
4.2 Gated Recurrent Unit
이때까지의 살펴본 RNN은 CPU가 작동하는 과정과 매우 유사하다고 볼 수 있다. 그러나 유사하다는 것은 concept적인 부분이고 실제 practical한 부분에서는 차이가 있다. 우리가 살펴본 RNN구조에서는 각 step에서 모든 memory가 refresh(update)된다는 점인데, CPU에서는 memory중 사용되는 값과 사용되지 않는 값이 다르게 refresh된다.
이런 CPU의 계산 과정을 mathmatical하게 표현하면 아래와 같이 표현할 수 있다.
여기서 $\odot$은 element-wise multiply를 의미한다.
위 식은 실제 사용되는 메모리가 아니라 candidate memory로 memory값으로 사용 될 수 있는 memory를 의미한다. 실제 메모리의 수식은 다음과 같다.
수식을 보면 아직 소개하지 않은 값들이 있는데 $\mathbf{r, u}$이다.
이 두값은 다음과 같이 표현될 수 있다.
이 식들 중 $\tilde{h}_t$를 구하는 식을 reset gate라 부르고, $h_t$를 구하는 식을 update gate라 부른다.
이제 우리가 알아볼 GRU에 대해서 살펴보자. GRU의 경우에는 위의 CPU가 working하는 과정과 매우 유사하다. 하지만 차이점에 대해서 먼저 생각해보면 우선 GRU의 경우 CPU처럼 instruction들에 대한 정보가 없어서 $\mathbf{u,r}$를 미리 setting 할 수 없다.
그리고 또 큰 차이점이자 문제점이라 할 수 있는 부분은 $\mathbf{u,r}$를 binary하게 0,1 값으로만 준다면 학습 시 미분값이 거의 대부분 0이 되서 학습을 할 수 없다.
따라서 두 벡터를 binary한 값이 아닌, [0,1]의 값을 가지는 real valued vector로 만든다.
그리고 다음과 같은 식이 최종적으로 완성된다.
그리고 각 step 에서 update는 다음과 같이 진행됩니다.
전체적인 구조와 각 계산들에 대해 하나씩 그림으로 보겠습니다. 그림의 출처는 이곳이며 소개한 수식에서 $\mathbf{u}$가 $\mathbf{v}$로 표현됬다는 차이가 있습니다.
- 전체 구조
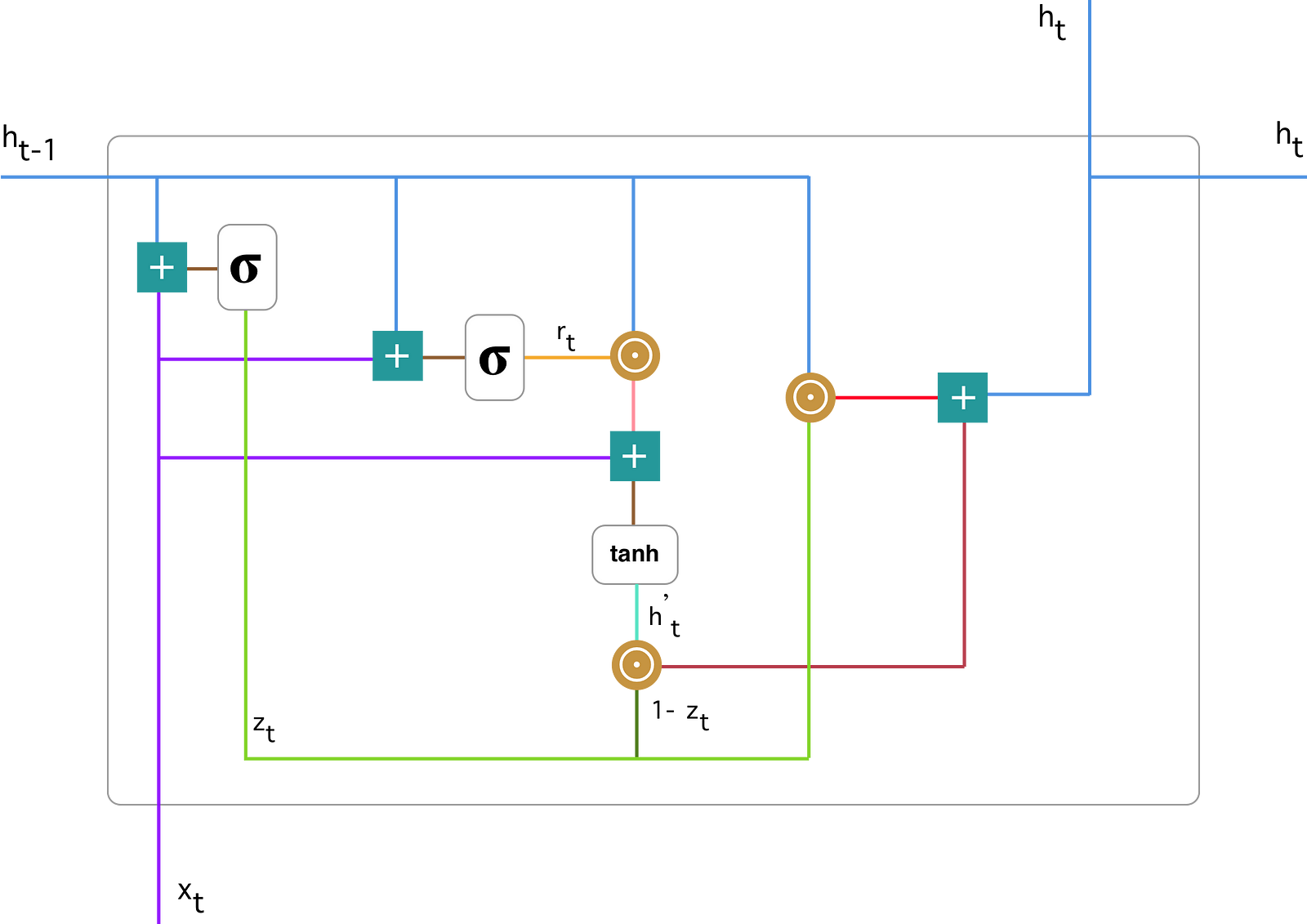
- Update Gate
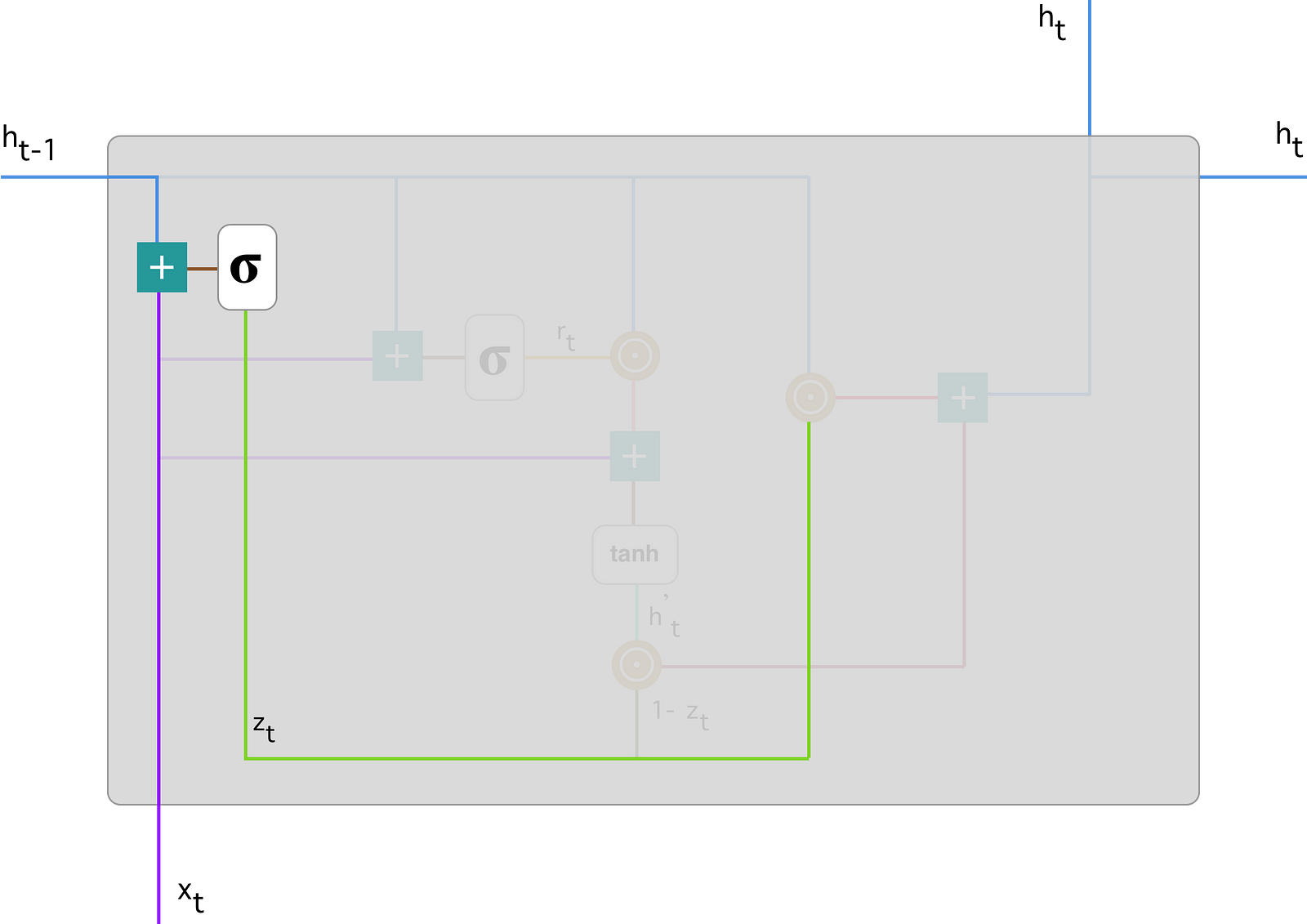
- Reset Gate
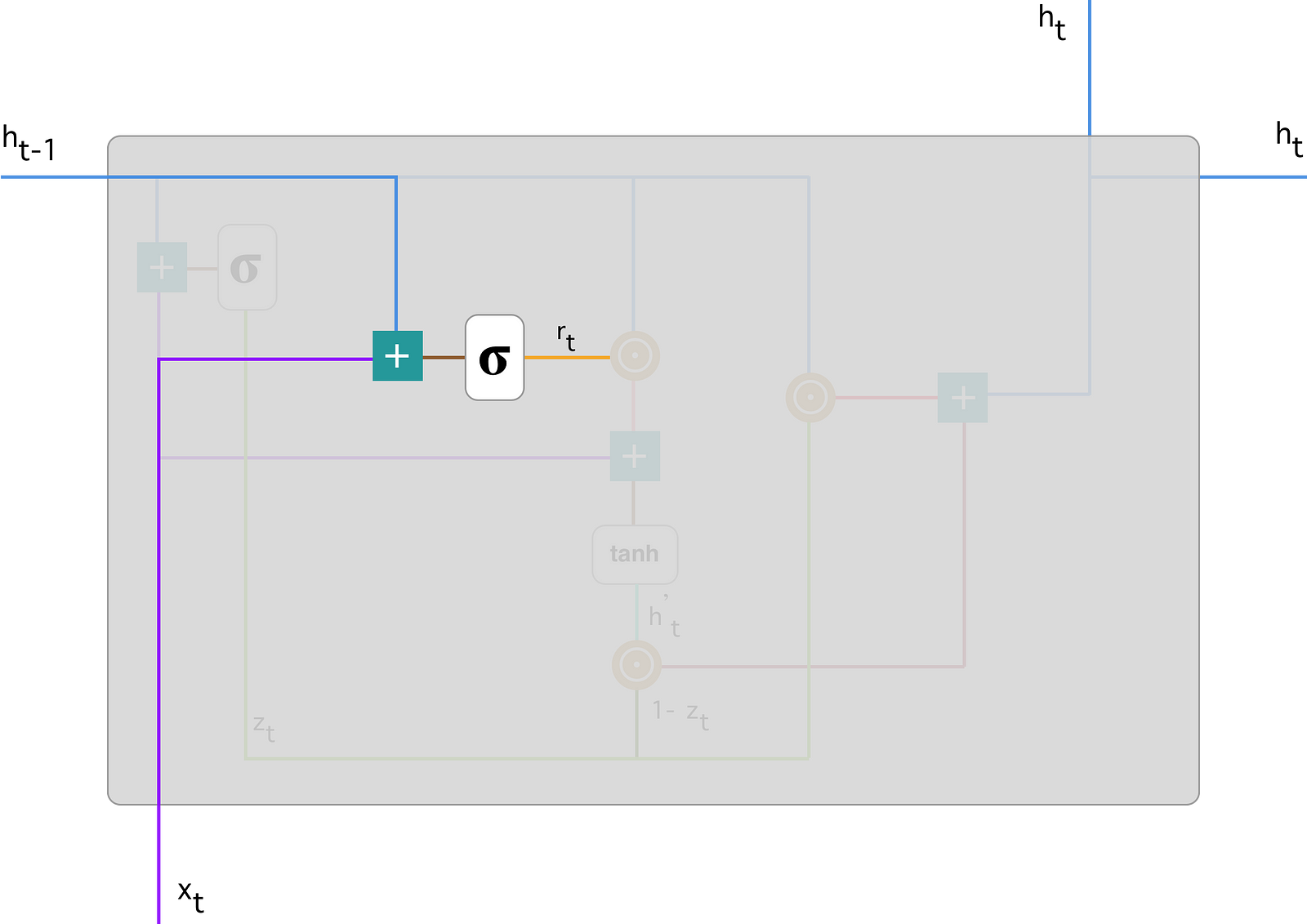
- cadidate memory
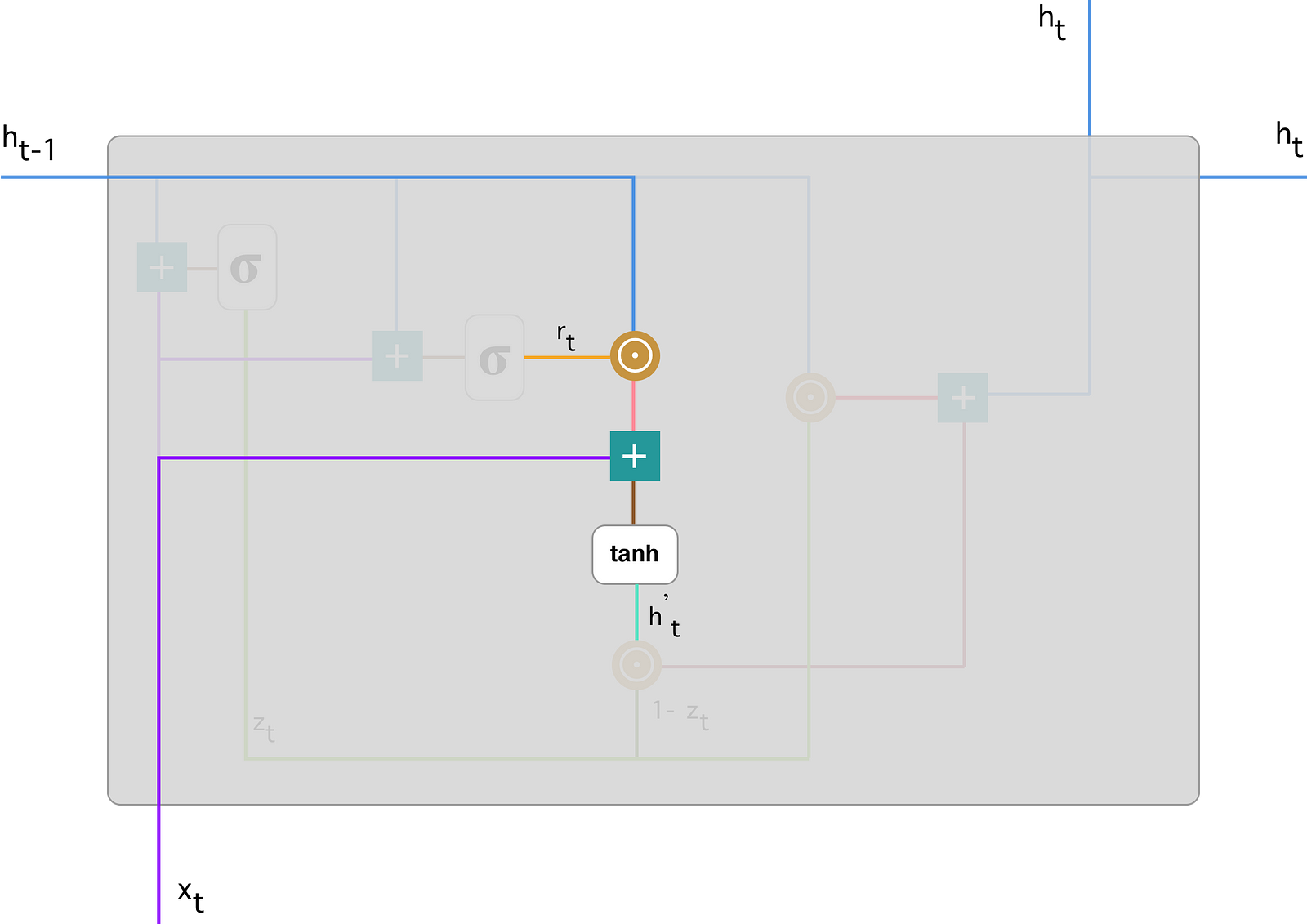
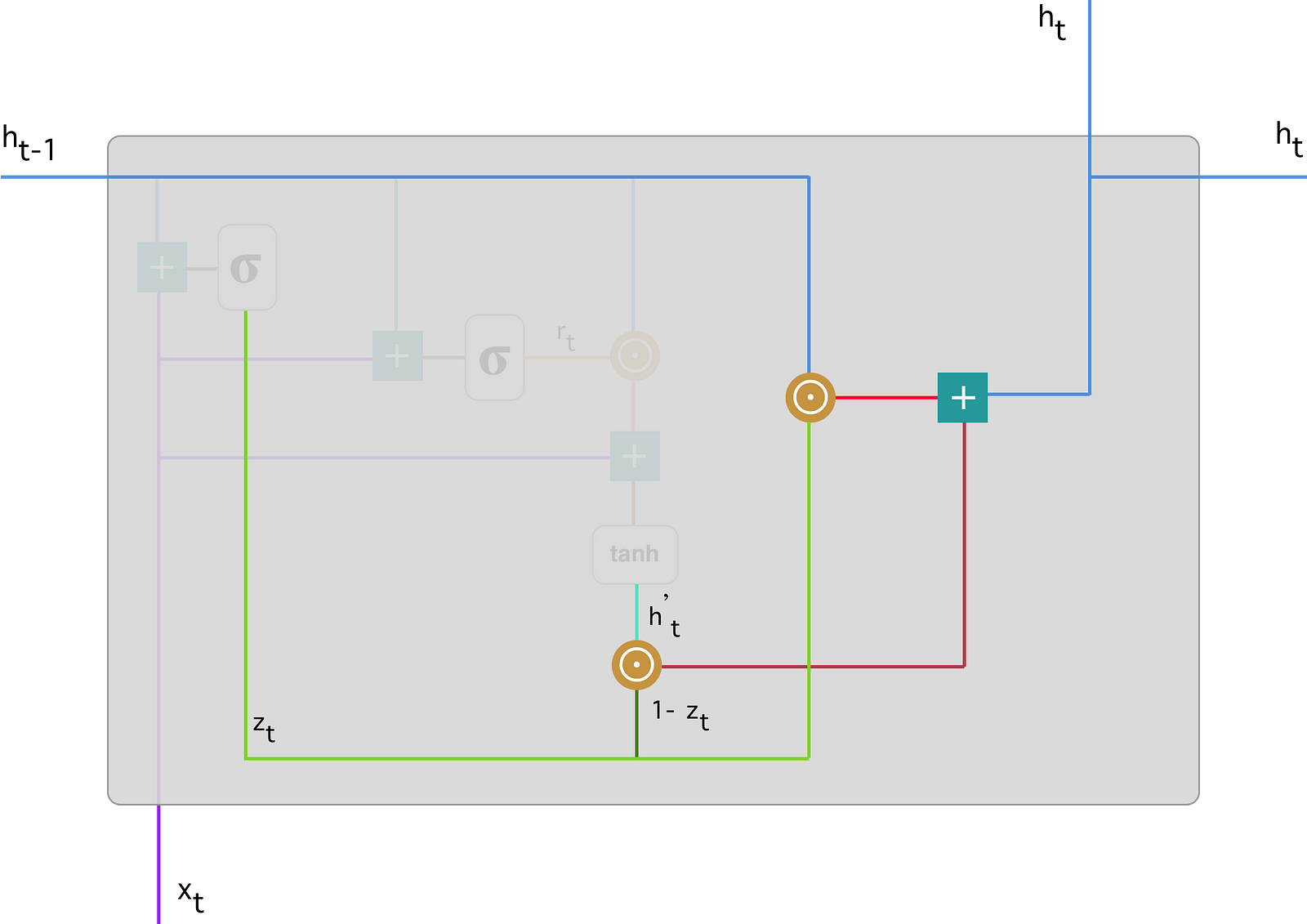
- Final memory
4.2.3 Long Short-Term Memory(LSTM)
위의 GRU는 LSTM을 motive로 만들어진 network이다.
LSTM과 GRU의 차이는 LSTM은 memory state $c_t$와 output $h_t$를 분리했다는 점이다. 이 책에는 LSTM에 대한 설명이 많지 않아서 다음 포스트에서 LSTM에 대해 따로 소개하도록 한다.
4.3 Why not Rectifiers?
GRU의 구조를 보면 활성화 함수로 sigmoid와 tanh를 사용했다는 점을 알 수 있다.
sigmoid의 경우에는 0~1값을 출력을 위해 사용했다고 이해 할 수 있지만, tanh같은 경우에는 CNN에서 좋은 성능을 보이는 Rectify계열의 활성화 함수(e.g. maxout,ReLU)를 사용하지 않은 이유에 대해 알아보도록 한다.
아래의 식을 보자. 이전에 소개된 식이다.
이 식에서 함수 $g()$는 활성화 함수이다. 이 함수를 다음과 같은 Recifier함수를 사용해 보자.
그리고 마지막 output을 계산하기 위한 값이자 memory인 $h_l$을 계산해보고 그 값의 norm을 계산해보자.
이 계산과정에 대한 다른 설명은 따로 하지 않고 lecture note에 나온 계산 과정만 확인한다.



다음의 식에서 알 수 있는 것은 Rectify계열의 함수는 unbounded 하다는 특성이 있다. 따라서 RNN의 특성상 연쇄적으로 곱해진다면 norm은 기하급수적으로 증가하게 된다. 따라서 마지막 메모리인 $h_l$값이 무한대로 발산하게 된다.
이러한 문제점들 때문에 unbounded한 함수를 사용하지 않고 bounded된 sigmoid 혹은 unbounded한 함수를 활성화 함수로 사용한다.
4.3.2 Is tanh a Blessing?
이전 section에서 rectify계열의 활성화 함수를 사용하는 것 보다 sigmoid 또는 tanh를 사용해야 한다는 것을 확인했다. 그렇다면 tanh(혹은 sigmoid)의 경우는 항상 좋은 점만 있는지 살펴보자.
일반적으로 RNN을 계산해 output을 계산할 때 까지는 큰 문제점 없이 계산된다. 하지만 학습과정에서 backpropagation을 하면 문제점이 발생한다.
여기서도 note에 소개된 계산 과정에 대해서는 설명하지 않겠다. 어떠한 과정인지만 설명을 하자면 Backpropagation에서 마지막 memory인 $h_l$에 대한 처음 memory인 $h_{l_0}+1$로 미분한 값의 norm을 구하는 과정이다. 아래를 보도록 하자.

이 식에서 의미하는 것은 $\mathbf{U}$의 eigenvalue의 최대값이 $\frac1\lambda$보다 크다면 미분값이 무한대로 갈 것이고, 반대의 경우에는 0으로 수렴한다는 내용이다.
즉 tanh를 사용한 경우 feedforward계산에는 크게 문제가 없지만 backpropagation과정에서 gradient exploding 과 gradient vanishing 이 발생한다는 문제점이 있다.
4.3.3 Are We Doomed?
- Exploding Gradient
이전 section에서 gradient가 exploding하는 문제에 대해 확인했다. 그렇다면 이러한 문제를 해결하는 방법은 무었일까?
다행이도 이러한 문제를 해결하는 것은 어렵지 않다. Cost에 대한 gradient 값을 계속해서 확인해서 일정한 임계값($\tau$)을 넘어 갈 경우 이 값을 줄여주면 된다. 여기서는 다음과 같은 식이 사용된다.
이러한 방법은 gradient clippikng이라고도 불린다.
- Vanishing Gradient
Vanishing gradient는 exploding과 다르게 큰 문제점으로 받아들여진다.
gradient가 vanishing하는 과정에 대한 수식적인 소개가 note에는 나와있지만 여기서는 생략한다. vanishing gradient의 가장 큰 문제점은 이러한 문제를 해결할 방법이 거의 없다는 것이다. 그리고 우리는 vanishing gradient가 어떤 원인으로 발생하는지 구별하는 것이 어렵다. 예를 들면, lack of dependency에 의한 것인지, 혹은 underlying function때문인지 아니면 parameter setting이 잘못된 것인지 구분하기가 어렵다.
Chapter 4
Recurrent Neural Networks and Gated Recurrent Units
이 내용은 Newyork University의 조경현교수님의 NLP_DL강의 lecture note중 Recurrent Neural Networks and Gated Recurrent Units단원을 정리한 내용이다.
이번 단원에는 몇 개의 단원에서 생략된 부분이 있습니다. 전체적인 흐름에 있어선는 문제가 없다고 판단되는 선에서 생략했으나, 혹시나 생략된 부분에 알고 싶으신 분들은 lecture note를 참고해 주시기 바랍니다.
4.1 Recurrent Neural Network
기존의 우리가 배운 Neural Network에서는 input $x$가 고정 size의 scalar 혹은 vector였다. 그러나 여기서는 input $x$가 고정 size라는 가정을 없에고 가변 길이의 input, 즉 sequence를 다루는 법을 알아 볼 것이다.
우선 가장 간단한 형태인 binary값을 가지는 sequence에 대해서 살펴보자. 1 혹은 0 만을 가지는 sequence에 대해서 1의 개수를 알고 싶다면 어떻게 해야 할까? 이 때 사용해야 하는 함수는 다음과 같다.

위 알고리즘을 사용한다면 sequence에서의 1값이 몇번인지 확인 할 수 있을 것 이다. ADD1 알고리즘의 중요한 특징은 다음과 같다.
- ‘1’의 개수를 새는 memory $s$
- sequence의 각 symbol에 ‘하나씩’ 적용된다.(차례대로)
이 두가지 특성 때문에 가변길이의 sequence에 사용될 수 있다. 이 ADD1 알고리즘의 idea(‘memory’&’recursive function’)를 일반화 하자. 가장 일반적인 예는 컴퓨터이다. 특히 컴퓨터에서 CPU가 명령어를 처리하는 과정에 위의 idea가 사용되었다. (CPU : sequence of instruction($x_i$)) 그러나 우리가 필요한 것은 학습을 위한 Network이므로 parametric recursive function (NLP를 하기 위한 언어적 symbol을 읽을 수 있는)가 필요하다.
Parametric recursive function을 만들기 위해 필요한 것에 대해 먼저 생각해보자. 우선 memory역할을 할 vector가 필요하다 이를 $h\in\mathbb{R}^{d_h}$라 하자. 그리고 recursive한 fucntion은 input symbol과 memory $h$ 둘 다 input으로 받는다. 이후 function을 통과시켜 memory를 업데이트 시킨 후 return한다. 각각의 memory $h$를 구분하기 위해 time index을 사용한다. ($h_t,h_{t-1},…$) 이러한 recursive한 fucntion은 다음과 같이 작성될 것이다.
그리고 함수 $f()$는 다음과 같이 정의한다.
- $\phi(~~)$함수는 input symbol을 d dimension으로 바꿔주는 함수.
- $W\in\mathbb{R}^{d_h\times d}$
- $U\in\mathbb{R}^{d_h\times d_h}$
- $g$는 element-wise nonlinear한 activation function뭐든 사용가능 하다.(e.g $tanh, sigmoid$)
위의 함수를 통과하게 되면 $d_h$ dimension을 가지는 vector가 된다. 이 값은 다음 값의 memory로 사용되거나 output으로 사용된다.
함수에 대해서 정의했으므로 이제는 두 가지 분류로 문제를 구분할 것이다.
- fixed-size의 output $y$
- variable length sequence의 output $y$
4.1.1 Fixed size output
기본적인 binary classification의 경우에 대해서 살펴보자. 가장 대표적인 binary classification의 예는 글에 대해 positive(1), negative(0) 감정을 평가하는 문제다. 이러한 문제는 결과가 0 혹은 1이므로 bernoulli distribution이라 생각할 수 있다. 따라서 우리는 distribution의 유일한 parameter인 $\mu$만 구하면 된다. 따라서 $\mu$를 다음과 같이 정의한다.
- 마지막 memory인 $h_l$사용
- 활성화 함수로 sigmoid 함수 사용한다.(0~1값을 출력해야 하므로)
따라서 전체적인 계산은 다음과 같이 한다.
여기서 가장 최초의 memory인 $h_0$는 보통 all zero vector를 사용한다. 그리고 $\mathbf{W, U}$는 shared parameter다.
또 다른 예를 들어 보자. 이번에도 감정 분석 문제이지만, 이번에는 분석해야 할 class가 3개, 즉 positive(1), neutral(2), neagtive(3)으로 분석해야 하는 문제에 대해 살펴보자. 이번에는 출력값이 $\mu$값 1개가 아닌, 3개의 $\mu$를 가지는 $\mathbf{\mu}= [\mu_1, \mu_2, \mu_3]$벡터를 출력으로 구해야 한다. 구하는 방식은 이전과 거의 비슷하지만 마지막 output을 뽑아낼 때 sigmoid가 아닌 softmax를 사용해야 한다.
4.1.4 Variable length output
가변길이의 output은 sequence형태가 된다.
이러한 문제의 대표적인 예는 POS tagging 문제다. 각 input $x$에 대해 noun, verb, adjective, others에 대한 각각의 확률값을 출력하는 문제다.
이러한 경우에는 각각의 step에서 memory를 각 step의 출력층, 다음 step 두 곳 모두로 보낸다. 각각의 layer에서의 출력은 다음과 같이 계산한다.
학습을 위해 각 step의 Cost는 다음과 같이 정의한다.
Cost함수에 대해서 간단히 설명을 하자면 I함수 때문에 정답 label을 가지는 단어에 대해서만 log값을 계산한다. 이 때 -log함수이기 떄문에 1에 가까울수록 적은 Cost를 가지고, 0에 가까울 수록 매우 큰 Cost를 가지게 된다. 따라서 전체적으로 우리는 Cost를 minimize하는 방향으로 가야 한다.
Cost 계산을 실제로 할때는 총합을 계산해서 학습을 시킨다.
위의 전체 cost를 minimize하는 방향으로 Network를 학습시켜야 한다.
결국 이 식이 목표하는 것은
이 조건부 확률을 최대화 하는 것이다. 그러나 위의 식을 단순히 cost함수로 표현을 하기에는 각각의 $x$ value들이 independent하다는 가정이 필요하다. 그러나 대부분의 경우에 그러한 가정을 사용하기에는 무리가 있다. 예를 들어 POS tagging 의 경우에만 봐도 명사 뒤에는 동사가 나올 확률이 높아진다. 이런 경우만 봐도 $x$ value들은 independent라고 하기는 어렵다. 따라서 우리는 condition으로 $y$의 값도 사용함으로써 독립 가정에 의한 격차를 줄인다. 즉, 아래와 같은 식으로 계산한다.
4.2 Gated Recurrent Unit
이때까지의 살펴본 RNN은 CPU가 작동하는 과정과 매우 유사하다고 볼 수 있다. 그러나 유사하다는 것은 concept적인 부분이고 실제 practical한 부분에서는 차이가 있다. 우리가 살펴본 RNN구조에서는 각 step에서 모든 memory가 refresh(update)된다는 점인데, CPU에서는 memory중 사용되는 값과 사용되지 않는 값이 다르게 refresh된다. 이런 CPU의 계산 과정을 mathmatical하게 표현하면 아래와 같이 표현할 수 있다.
여기서 $\odot$은 element-wise multiply를 의미한다. 위 식은 실제 사용되는 메모리가 아니라 candidate memory로 memory값으로 사용 될 수 있는 memory를 의미한다. 실제 메모리의 수식은 다음과 같다.
수식을 보면 아직 소개하지 않은 값들이 있는데 $\mathbf{r, u}$이다. 이 두값은 다음과 같이 표현될 수 있다.
이 식들 중 $\tilde{h}_t$를 구하는 식을 reset gate라 부르고, $h_t$를 구하는 식을 update gate라 부른다.
이제 우리가 알아볼 GRU에 대해서 살펴보자. GRU의 경우에는 위의 CPU가 working하는 과정과 매우 유사하다. 하지만 차이점에 대해서 먼저 생각해보면 우선 GRU의 경우 CPU처럼 instruction들에 대한 정보가 없어서 $\mathbf{u,r}$를 미리 setting 할 수 없다. 그리고 또 큰 차이점이자 문제점이라 할 수 있는 부분은 $\mathbf{u,r}$를 binary하게 0,1 값으로만 준다면 학습 시 미분값이 거의 대부분 0이 되서 학습을 할 수 없다. 따라서 두 벡터를 binary한 값이 아닌, [0,1]의 값을 가지는 real valued vector로 만든다.
그리고 다음과 같은 식이 최종적으로 완성된다.
그리고 각 step 에서 update는 다음과 같이 진행됩니다.
전체적인 구조와 각 계산들에 대해 하나씩 그림으로 보겠습니다. 그림의 출처는 이곳이며 소개한 수식에서 $\mathbf{u}$가 $\mathbf{v}$로 표현됬다는 차이가 있습니다.
- 전체 구조

- Update Gate

- Reset Gate

- cadidate memory

- Final memory

4.2.3 Long Short-Term Memory(LSTM)
위의 GRU는 LSTM을 motive로 만들어진 network이다. LSTM과 GRU의 차이는 LSTM은 memory state $c_t$와 output $h_t$를 분리했다는 점이다. 이 책에는 LSTM에 대한 설명이 많지 않아서 다음 포스트에서 LSTM에 대해 따로 소개하도록 한다.
4.3 Why not Rectifiers?
GRU의 구조를 보면 활성화 함수로 sigmoid와 tanh를 사용했다는 점을 알 수 있다. sigmoid의 경우에는 0~1값을 출력을 위해 사용했다고 이해 할 수 있지만, tanh같은 경우에는 CNN에서 좋은 성능을 보이는 Rectify계열의 활성화 함수(e.g. maxout,ReLU)를 사용하지 않은 이유에 대해 알아보도록 한다.
아래의 식을 보자. 이전에 소개된 식이다.
이 식에서 함수 $g()$는 활성화 함수이다. 이 함수를 다음과 같은 Recifier함수를 사용해 보자.
그리고 마지막 output을 계산하기 위한 값이자 memory인 $h_l$을 계산해보고 그 값의 norm을 계산해보자. 이 계산과정에 대한 다른 설명은 따로 하지 않고 lecture note에 나온 계산 과정만 확인한다.
다음의 식에서 알 수 있는 것은 Rectify계열의 함수는 unbounded 하다는 특성이 있다. 따라서 RNN의 특성상 연쇄적으로 곱해진다면 norm은 기하급수적으로 증가하게 된다. 따라서 마지막 메모리인 $h_l$값이 무한대로 발산하게 된다.
이러한 문제점들 때문에 unbounded한 함수를 사용하지 않고 bounded된 sigmoid 혹은 unbounded한 함수를 활성화 함수로 사용한다.
4.3.2 Is tanh a Blessing?
이전 section에서 rectify계열의 활성화 함수를 사용하는 것 보다 sigmoid 또는 tanh를 사용해야 한다는 것을 확인했다. 그렇다면 tanh(혹은 sigmoid)의 경우는 항상 좋은 점만 있는지 살펴보자.
일반적으로 RNN을 계산해 output을 계산할 때 까지는 큰 문제점 없이 계산된다. 하지만 학습과정에서 backpropagation을 하면 문제점이 발생한다.
여기서도 note에 소개된 계산 과정에 대해서는 설명하지 않겠다. 어떠한 과정인지만 설명을 하자면 Backpropagation에서 마지막 memory인 $h_l$에 대한 처음 memory인 $h_{l_0}+1$로 미분한 값의 norm을 구하는 과정이다. 아래를 보도록 하자.
이 식에서 의미하는 것은 $\mathbf{U}$의 eigenvalue의 최대값이 $\frac1\lambda$보다 크다면 미분값이 무한대로 갈 것이고, 반대의 경우에는 0으로 수렴한다는 내용이다.
즉 tanh를 사용한 경우 feedforward계산에는 크게 문제가 없지만 backpropagation과정에서 gradient exploding 과 gradient vanishing 이 발생한다는 문제점이 있다.
4.3.3 Are We Doomed?
- Exploding Gradient
이전 section에서 gradient가 exploding하는 문제에 대해 확인했다. 그렇다면 이러한 문제를 해결하는 방법은 무었일까? 다행이도 이러한 문제를 해결하는 것은 어렵지 않다. Cost에 대한 gradient 값을 계속해서 확인해서 일정한 임계값($\tau$)을 넘어 갈 경우 이 값을 줄여주면 된다. 여기서는 다음과 같은 식이 사용된다.
이러한 방법은 gradient clippikng이라고도 불린다.
- Vanishing Gradient
Vanishing gradient는 exploding과 다르게 큰 문제점으로 받아들여진다. gradient가 vanishing하는 과정에 대한 수식적인 소개가 note에는 나와있지만 여기서는 생략한다. vanishing gradient의 가장 큰 문제점은 이러한 문제를 해결할 방법이 거의 없다는 것이다. 그리고 우리는 vanishing gradient가 어떤 원인으로 발생하는지 구별하는 것이 어렵다. 예를 들면, lack of dependency에 의한 것인지, 혹은 underlying function때문인지 아니면 parameter setting이 잘못된 것인지 구분하기가 어렵다.
Comments